Sigmoid
Sigmoid函数在定义域内处处可导,当sigmoid 函数输入的值趋于正无穷或负无穷时,梯度会趋近零,在反向传播的过程中,导致了向低层传播的梯度也变得非常小,训练很难进行,即产生了梯度消失现象。而且,sigmoid函数的输出恒为正值,不是以零为中心的,这会导致权值更新时只能朝一个方向更新,从而影响收敛速度。
一般sigmoid函数只用于二分类的输出层。

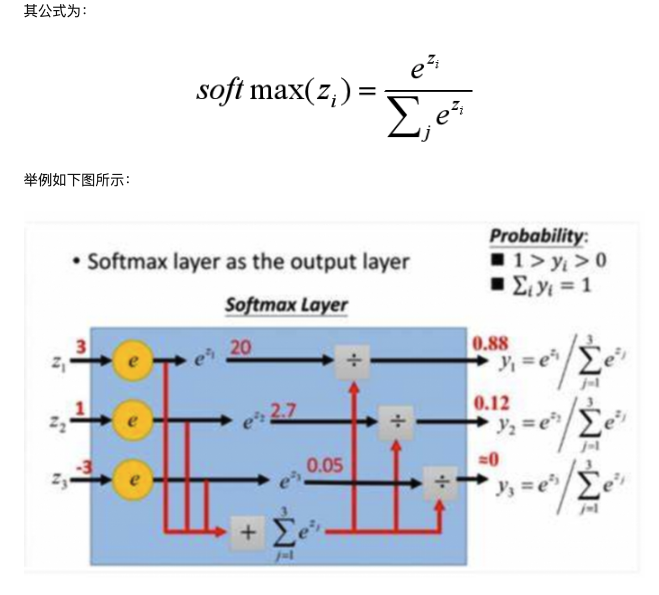
Softmax
Softmax常用于多分类问题中,他是二分类函数sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来,同时,可以将为负值的输出转化为正的概率值。 某一样本对于三个分类类别的输出为(3,1,-3),经过softmax激活函数,y1的输出为:
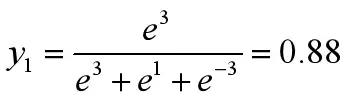
经过计算输出变为(0.88,0.12,0),这表示该样本大概率将属于第一个类别。
Softmax本质是将网络输出值映射到(0,1)区间,这些值的和为1,我们便可以将其理解为概率,概率最大的类别,就是该样本所属的类别。
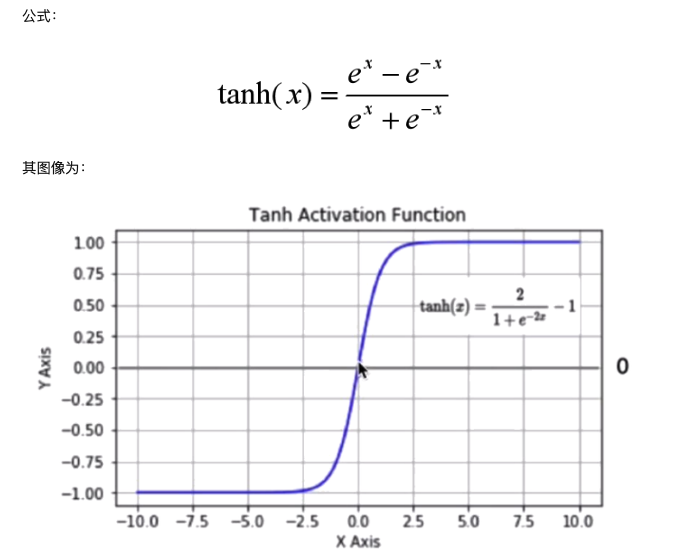
Tanh 双曲正切曲线
Tanh与sigmoid相比,是以0为中心的,这使得其收敛速度比sigmoid快,同时可以减少迭代次数。但是,当输入的值趋于正无穷或负无穷时,tanh的梯度同样会趋近零,造成梯度消失。
使用时可以在隐藏层使用tanh函数,在输出层使用sigmoid函数。
Relu
ReLu函数是目前最常用的激活函数。当x<0时,其导数为0,当x>0时,导数恒定,所以可以解决梯度消失问题。而且,ReLu会使一部分神经元的输出为0,这样会造成网格的稀疏性,减少参数的相互依存关系,缓解了过拟合问题的发生。

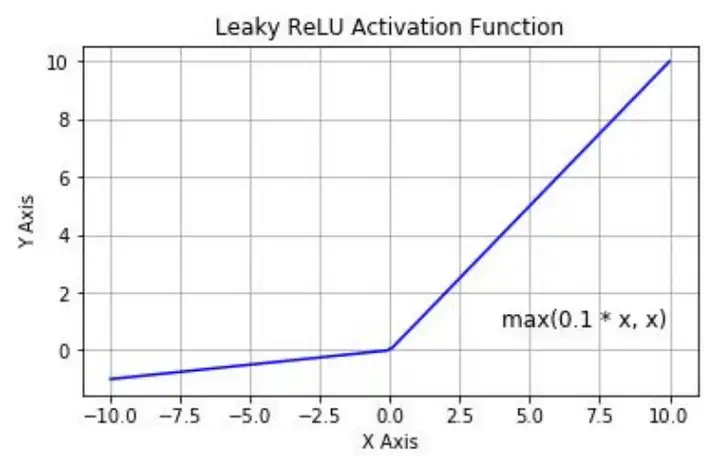
LeakyReLu:带泄露线性整流 Relu的输入值为负的时候,输出始终为0,其一阶导数也始终为0,这样会导致神经元对应权重不能更新,造成“神经元死亡”的现象。为了解决Relu函数这个缺点,在Relu函数的负半区间引入一个泄露(Leaky)值作为斜率,使得在负区间仍然有较小梯度,LeakyReLu函数是对ReLu的改进,其公式为:
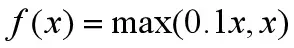
(负半轴的Leaky值可以选取别的值,称为带泄露随机线性整流(RReLu))
其图像为:
Strategy
如何选择激活函数:
隐藏层:
1)优先选择ReLu函数,如果效果不好,尝试其他,比如LeakyReLu;
2)不要使用sigmoid函数,可以尝试tanh函数。
输出层:
1)二分类问题选择sigmoid函数;
2)多分类问题选择softmax函数;
3)回归问题选择identity函数。(f(x)=x)